過去記事に記載のとおり、RAMS 2026は、2025年1月19日から23日まで、昨年と同じく米国フロリダ州ミラマービーチのヒルトンサンデスティンホテルで開催されました。弊社代表は初日に論文発表を行いました。

本論文のタイトルは、"LLM Optimized Fault Tree Analysis (LOFTA) for Probabilistic Metric for Random Hardware Failures (PMHF) under ISO 26262"です。邦題は「ISO 26262に基づくランダムハードウェア故障確率指標（PMHF）のためのLLM最適化故障木解析（LOFTA）」になります。

今回のRAMS 2026の論文では、LLMでシステムのブロック図からフォールトツリーを自動生成します。さらに、FTAで算出したPMHFへの寄与をLLMで解析し、アーキテクチャの弱点を特定し改善する手法を提案しています。

提案手法は自動化による省力化だけでなく、車載システム全体の信頼性向上にも寄与します。本研究により、ADASや自動運転などのセーフティクリティカルな応用において、解析効率の向上と設計の最適化が図られます。

前のブログ 次のブログ

弊社コンテンツの12月の検索結果です。

前のブログ 次のブログ

弊社コンテンツの11月の検索結果です。

前のブログ 次のブログ

弊社コンテンツの10月の検索結果です。

前のブログ 次のブログ

On October 30, 2025, FS Micro Corporation※1, a provider of ISO 26262※2 consulting, announced that a paper authored by its President and CEO, Atsushi Sakurai, was accepted to RAMS 2026※3, a global conference organized by the IEEE※4 Reliability Society.

This marks Sakurai’s seventh consecutive acceptance at RAMS since 2020. The paper is scheduled to be presented at RAMS 2026 in Florida, USA, in January 2026, and has also been named a finalist for the Best Paper Award.

Beginning with an acceptance at an IEEE conference in 2017, Sakurai proposed a higher-accuracy PMHF※5 formulation at RAMS 2020 and has since continued contributions, including proposals to correct issues in the published formulae.

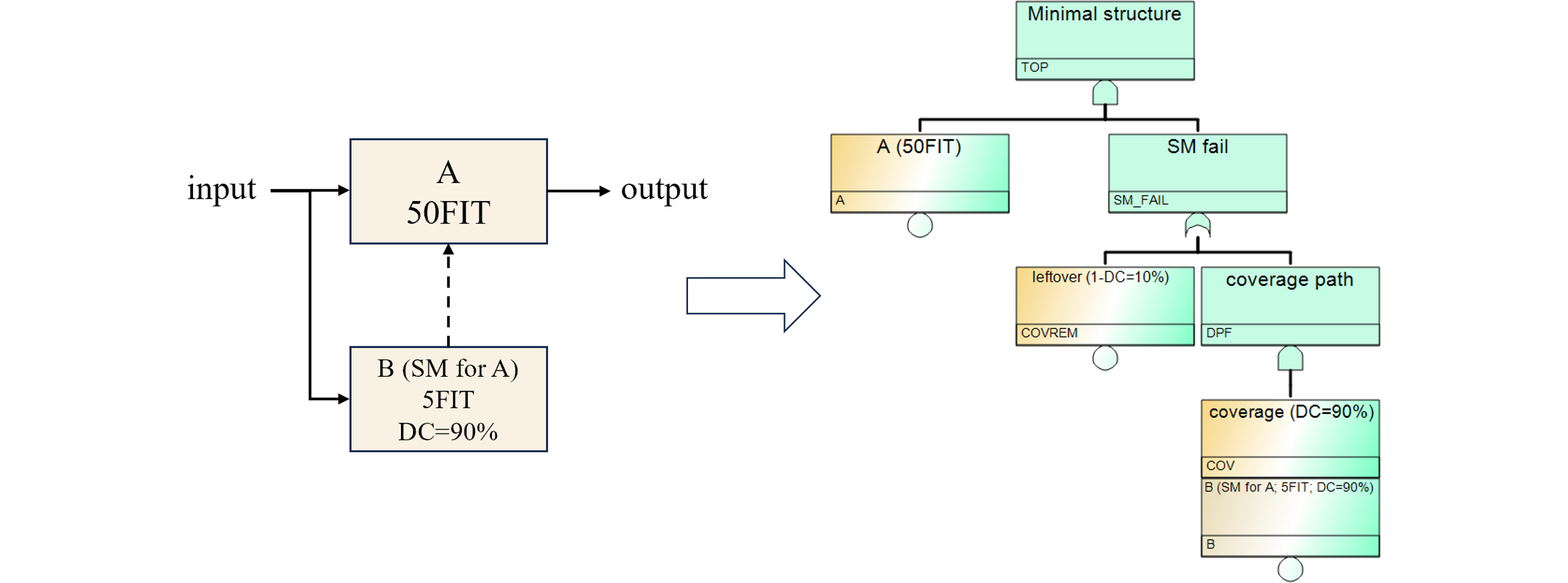
In the RAMS 2026 paper, an LLM※6 is used to automatically generate a fault tree※7 from a system block diagram. The method then analyzes, with an LLM, each component’s contribution to PMHF computed via FTA※8, thereby identifying and improving architectural weaknesses.

The proposed approach not only reduces engineering effort through automation but also contributes to improved system-level reliability in automotive electronics. Based on this research, ADAS※9 and autonomous-driving applications can achieve higher analysis efficiency and more optimized system design.

Notes
※1 FS Micro Corporation. Head Office: Nagoya. President and CEO: Atsushi Sakurai. Consulting for functional safety of automotive electronic systems. https://fs-micro.com/
※2 ISO 26262. International standard for functional safety of road-vehicle electric and electronic systems. Its goal is to reduce the risk of hazardous events during vehicle operation to an acceptable level.
※3 RAMS, Reliability and Maintainability Symposium. International conference on reliability engineering organized by the IEEE Reliability Society and partners. The 72nd symposium will be held in Florida, USA, in 2026. https://rams.org/
※4 IEEE, Institute of Electrical and Electronics Engineers. One of the world’s largest professional organizations advancing technology. https://ieee.org/
※5 PMHF, Probabilistic Metric for Random Hardware Failures. Time-average probability of dangerous failures from random hardware faults, used as a hardware design target in ISO 26262.
※6 LLM, Large Language Model. AI models trained on large text corpora for natural-language understanding and generation.
※7 Fault Tree. Logical tree representing causal pathways of system failures, useful for revealing structural vulnerabilities.
※8 FTA, Fault Tree Analysis. Systematic reliability analysis based on a fault tree, used to derive minimal cut sets and contribution measures for design improvement.
※9 ADAS, Advanced Driver Assistance Systems. Driver-assistance functions such as ACC adaptive cruise control, AEB automatic emergency braking, LKA lane keeping assist, a domain with stringent safety requirements.

Contact
Company: FS Micro Corporation
Representative: Atsushi Sakurai
Established: August 21, 2013
Capital: JPY 32,000,000 (including capital reserve)
Business: Consulting and seminars on functional safety for ISO 26262 automotive electronic systems
Email: info@fs-micro.com
URL: https://fs-micro.com/

前のブログ 次のブログ

2025年10月30日、ISO 26262※1のコンサルティングを提供するFSマイクロ株式会社※2は、代表取締役 桜井 厚の論文が、IEEE※3信頼性部会が主催する国際会議RAMS 2026※4に採択されたことを発表しました。

桜井の論文がRAMSに採択されるのは、2020年から今回で7年連続となります。この論文は2026年1月に米国フロリダ州で開催されるRAMS 2026において発表予定であり、最優秀論文候補にも指名されています。

桜井は2017年のIEEEでの論文採択に始まり、RAMS 2020ではより高精度なPMHF※5式を提案し、また、規格式自体の改善提案などを含め、ISO 26262に関する貢献を積み重ねてきました。

今回のRAMS 2026の論文では、LLM※6でシステムのブロック図からフォールトツリー※7を自動生成します。さらに、FTA※8で算出したPMHFへの寄与をLLMで解析し、アーキテクチャの弱点を特定し改善する手法を提案しています。

提案手法は自動化による省力化だけでなく、車載システム全体の信頼性向上にも寄与します。本研究により、ADAS※9や自動運転などのセーフティクリティカルな応用において、解析効率の向上と設計の最適化が図られます。

【注釈】
※1：ISO 26262：車載電気電子システムの機能安全に関する国際規格。運転中に生じ得る危険事象のリスクを許容水準まで低減することを目的とする。
※2：FSマイクロ株式会社（本社：名古屋市。代表取締役：桜井 厚）：車載システムの機能安全に関するコンサルティングを提供。https://fs-micro.com/
※3：IEEE（Institute of Electrical and Electronics Engineers、電気電子技術者協会）：技術の進歩を推進する世界最大級の専門技術者組織。https://ieee.org/
※4：RAMS（the Reliability and Maintainability Symposium）：IEEE信頼性部会などが主催する信頼性工学の国際会議。第72回は2026年に米国フロリダ州で開催予定。
※5：PMHF（Probabilistic Metric for Random Hardware Failures）：ランダムハードウェア故障に起因する危険側故障の時間平均確率を表す指標。ISO 26262でハードウェア設計目標として用いられる。https://rams.org/
※6：LLM（Large Language Model）：ChatGPTに代表される大規模言語モデル。大量データ学習により自然言語の理解と生成を行うAI技術。
※7：フォールトツリー（Fault Tree）：システム故障の原因を論理的に表現する木構造。イベントを論理ゲートで接続することでシステムの脆弱性の把握に役立つ。
※8：FTA（Fault Tree Analysis）：フォールトツリーに基づく体系的な信頼性解析手法。最小カット集合の抽出や寄与度評価などを通じて設計改善点を導出する。
※9：ADAS（Advanced Driver Assistance Systems）：自動車の運転支援機能群。例：ACC（適応型クルーズコントロール）、AEB（自動緊急ブレーキ）、LKA（車線維持支援）など。安全関連要求が高い領域に属する。

【お問い合わせ先】
会社名　　　　 FSマイクロ株式会社
代表者　　　　 桜井 厚
設立年月日　　 2013年8月21日
資本金　　　　 3,200万円(資本準備金を含む)
事業内容　　　 ISO 26262車載電子機器の機能安全のコンサルティングおよびセミナー
メールアドレス info@fs-micro.com
URL　　　　　 https://fs-micro.com/

前のブログ 次のブログ

弊社コンテンツの9月の検索結果です。

前のブログ 次のブログ

10/1に最終的に査読に対応した、所属と氏名有りの論文をシステムに登録しました。あとは審査結果を待つのみです。例年だと10月末頃に採択発表がある予定です。

前のブログ 次のブログ

初回の査読結果が返ってきました。修正はほぼ一か所だけで、本提案の名前を付けられるか？とのこと。 ChatGPTの助けも借りて、XXXという名称を付けて本提案を呼ぶことにしました。これにより、我々の提案を長いフレーズで呼ばなくても良くなりました。さらにプレゼン資料には多少追加が必要とのことで、数日中に対応予定です。

前のブログ 次のブログ

弊社コンテンツの7月の検索結果です。

前のブログ 次のブログ